Aljabar Boolean

- October 03, 2017

Aljabar Boolean adalah salah satu aljabar yang berkaitan dengan variabel-variabel biner dan operasi-operasi logika. Variabel-variabel dalam aljabar boole dinyatakan dengan huruf-huruf seperti : A, B, C, …, X, Y, Z. Sedangkan dalam aljabar Boolean terdapat 3 operasi logika dasar yaitu : AND, OR dan NOT (Komplemen).

Sebuah fungsi Boolean adalah sebuah ekspresi aljabar yang dibentuk dengan variabel-variabel biner, simbol-simbol operasi logika, tanda kurung dan tanda “=”. Untuk sebuah nilai yang diberikan pada variabel , fungsi Boolean dapat bernilai 1 atau 0.

Contoh fungsi Boolean :

f = X + Y ’ . Z

Fungsi f sama dengan 1 jika X = 1 atau jika kedua nilai Y ‘ dan Z = 1.

f = 0 dalam hal lain.

Tetapi kita juga dapat menyatakan bahwa jika Y ‘ = 1, maka Y = 0, karena Y ‘ adalah komplemen dari Y. Secara ekuivalen dapat dinyatakan bahwa :

f = 1

jika X = 1 atau Y.Z = 0.1

Hubungan antar sebuah fungsi dengan variabel-variabel binernya dapat disajikan dalam bentuk sebuah Tabel Kebenaran (Truth Table). Untuk menyajikan sebuah fungsi dalam sebuah tabel kebenaran, kita membutuhkan sebuah daftar 2ⁿ kombinasi 1 dan 0 dari n buah variabel biner.

Contoh :

f = X + Y ’ . Z

∑ variabel = 3 (X, Y’ dan Z)

2ⁿ = 23 = 8 kombinasi 0 dan 1.

Maka tabel kebenarannya adalah sebagai berikut :

X	Y	Y’	Z	Y ‘ .Z	f = X + Y ’ . Z
0	0	1	0	0	0
0	0	1	1	1	1
0	1	0	0	0	0
0	1	0	1	0	0
1	0	1	0	0	1
1	0	1	1	1	1
1	1	0	0	0	1
1	1	0	1	0	1

Sebuah fungsi Boolean dapat diubah menjadi sebuah diagram logika yang terdiri dari gerbang-gerbang logika.

Contoh :

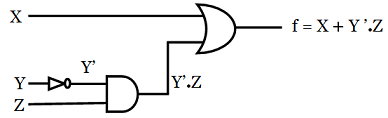
f = X + Y ’ . Z

Diagram logikanya :

Kegunaan dari aljabar Boolean adalah memberikan fasilitas penulisan dalam perancangan rangkaian digital. Aljabar Boole menyediakan alat untuk dibuat :

Mengekspresikan dalam bentuk aljabar sebuah tabel kebenaran yang merupakan hubungan antara variabel-variabel,
Mengekspresikan dalam bentuk aljabar hubungan input dan output diagram logika,
Mendapatkan rangkaian-rangkaian yang lebih sederhana untuk fungsi yang sama.

RELASI-RELASI DASAR ALJABAR BOOLEAN :

1. X + 0 = X	7. X + X’ = X	13. X.(Y+Z) = X.Y + X.Z
2. X + 1 = 1	8. X . X’ = 0	14. X + Y.Z = (X+Y) . (X+Z)
3. X . 0 = 0	9. X + Y = Y + X	15. (X + Y)’ = X’ . Y’
4. X . 1 = X	10. X . Y = Y . X	16. (X.Y)’ = X’ + Y’
5. X + X = X	11. X+(Y+Z) = (X+Y)+Z	17. (X’)’ = X
6. X . X = X	12. X.(Y.Z) = (X.Y).Z	18. X.(X+Y) = X
		19. X + (X.Y) = X

Keterangan :

Relasi (1), (2), (3) dan (4) disebut dengan Hukum penjalinan dengan konstanta.
Relasi (5) dan (6) disebut Hukum perluasan.
Relasi (7) dan (8) disebut Hukum komplementasi
Relasi (9) dan (10) disebut Hukum komutatif.
Relasi (11) dan (12) disebut Hukum asosiatif.
Relasi (13) dan (14) disebut Hukum distributif.
Relasi (14) tidak dapat digunakan dalam aljabar biasa, tetapi relasi ini sangat berguna dalam memanipulasi ekspresi-ekspresi aljabar boole.
Relasi (15) dan (16) disebut Dalil de Morgan.
Relasi (17) menyatakan jika suatu variabel dikomplemenkan sebanyak dua kali maka akan didapat nilai asli dari variabel tersebut.
Relasi (18) dan (19) disebut Hukum absorpsi.

DEFINISI ALJABAR BOOLEAN

Aljabar adalah sistem aljabar pada suatu himpunan S dengan dua operasi yaitu penjumlahan ( + ) dan perkalian ( . ) yang didefinisikan pada himpunan tersebut.

Misalkan terdapat :

Dua operator biner: + dan ⋅
Sebuah operator uner: ’.
B : himpunan yang didefinisikan pada operator +, ⋅, dan ’
0 dan 1 adalah dua elemen yang berbeda dari B.

Clue :

(B, +, ⋅, ’)

Maka, disebut Aljabar Boolean jika untuk setiap a, b, c ∈ B berlaku aksioma-aksioma atau postulat Huntington atau hukum-hukum berikut:

HUKUM-HUKUM ALJABAR BOOLEAN

1. Closure:

(i) a + b ∈ B
(ii) a ⋅ b ∈ B

2. Identitas:

(i) a + 0 = a
(ii) a ⋅ 1 = a

3. Idempoten:

(i) a + a = a
(ii) a ⋅ a = a

4. Komplemen:

(i) a + a’ = 1
(ii) aa’ = 0

5. Dominansi:

(i) a ⋅ 0 = 0
(ii) a + 1 = 1

6. Involusi:

(i) (a’)’ = a

7. Penyerapan:

(i) a + ab = a
(ii) a(a + b) = a

8. Komutatif:

(i) a + b = b + a
(ii) ab = ba

9. Asosiatif:

(i) a + (b + c) = (a + b) + c
(ii) a (b c) = (a b) c

10 Distributif:

(i) a + (b c) = (a + b) (a + c)
(ii) a (b + c) = a b + a c

11. De Morgan:

(i) (a + b)’ = a’b’
(ii) (ab)’ = a’ + b’

12. Hukum 0/1:

(i) 0’ = 1
(ii) 1’ = 0

Contoh:
Buktikan (i) a + a’b = a + b dan (ii) a(a’ + b) = ab

Penyelesaian:
(i) a + a’b = (a + ab) + a’b (Penyerapan)
= a + (ab + a’b) (Asosiatif)
= a + (a + a’)b (Distributif)
= a + 1 • b (Komplemen)
= a + b (Identitas)

(ii) adalah dual dari (i)

PRINSIP DUALITAS

Jika suatu kesamaan aljabar boolean B benar maka dual dari B ,diperoleh dengan cara mengganti setiap + dengan . atau sebaliknya dan mengganti 1 dengan 0 atau juga sebaliknya, juga bernilai benar.

APLIKASI ALJABAR BOOLEAN

A. Jaringan Pensaklaran (Switching Network)

Saklar, yaitu objek yang mempunyai dua buah keadaan; buka dan tutup. Tiga bentuk gerbang paling sederhana:

1. Output b hanya ada jika dan hanya jika x dibuka ⇒ x